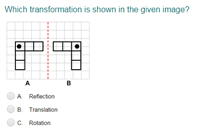
Rotational Symmetry
A figure has rotational symmetry if it can be rotated about a point less than a full turn and look the same as it did before the rotation.
The order of rotational symmetry is the number of times a figure looks the same as it did originally when it is rotated through 360°.
For example: Consider this figure.

If we rotate it one-half turn, it will look the same.

So, it has rotational symmetry.
Also, observe that when the figure is rotated through 360°, it looks the same two times.
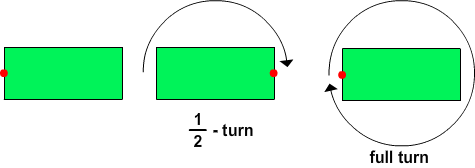
So, this figure has rotational symmetry of order 2.
Even if a figure has no rotational symmetry, the order of rotational symmetry will still be 1 as every figure looks the same at the end of a complete rotation (360°).
For example: Consider this figure.

The order of rotational symmetry of this figure is 1.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Help
The correct answer is
Remember :
The smallest number is the one that comes first while counting.
Solution :
To arrange the given numbers in order from smallest to greatest, find the smallest number among all the given numbers.
21,27,23
21 is the smallest number.