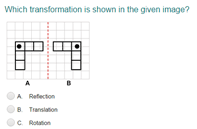
Rotational Symmetry

A figure has rotational symmetry if it can be rotated about a point less than a full turn and look the same as it did before the rotation.

The order of rotational symmetry is the number of times a figure looks the same as it did originally when it is rotated through 360°.

For example: Consider this figure.

If we rotate it one-half turn, it will look the same.

So, it has rotational symmetry.

Also, observe that when the figure is rotated through 360°, it looks the same two times.
 

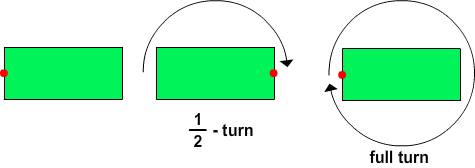
So, this figure has rotational symmetry of order 2.

Even if a figure has no rotational symmetry, the order of rotational symmetry will still be 1 as every figure looks the same at the end of a complete rotation (360°).

For example: Consider this figure.

The order of rotational symmetry of this figure is 1.