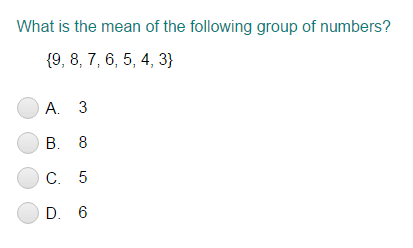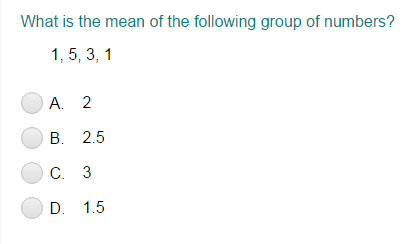Login as parent/teacher to assign this.
Mean
Lesson size:
Message preview:
Someone you know has shared lesson with you:
To play this lesson, click on the link below:
https://www.turtlediary.com/lesson/mean.html
To know more about different lessons, please visit www.turtlediary.com
Hope you have a good experience with this site and recommend to your friends too.
Login to rate activities and track progress.
Login to rate activities and track progress.
Statistics Games
Statistics Videos
Statistics Quizzes
Statistics Worksheets
Explore Even More Ways To Learn!
I'm looking for
about
for
Adblock Detected
Our team has worked hard to create this Fun Educational Website FREE of charge to users like you. It costs a great deal of money to do that. Please help us keep the website Free and continue the work.
OR
If you think, you got this page by mistake then Click here to send the feedback.